Inverse Kinematics Redoux

Published on 2017-03-18 in Deltabot.

Now that I have it working, I should explain the inverse kinematics of this delta arm properly. First, let’s just consider a single arm of the delta – the other two are going to be pretty much identical:

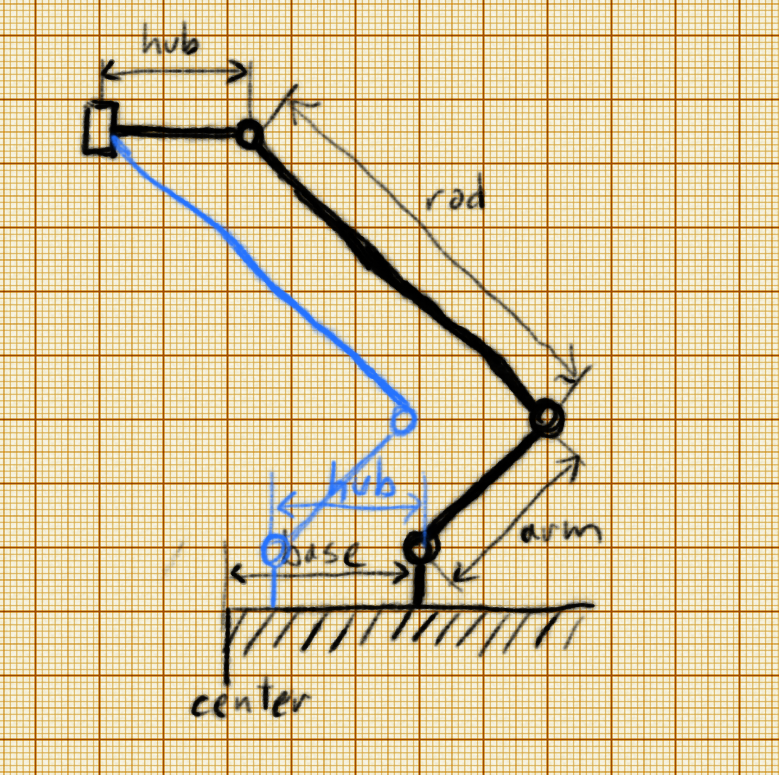
The_arm_ is attached to the servo at distance_base_ from the center of the robot. It connects to the_rod_, which in turns connects to 1/3 of the_hub_. At the center of the hub is the actual tool that we want to move.

We can make a very large simplification in our model. If we skip the_hub_, and simply assume that the rod is connected to the tool directly, we can shift the whole robot by the length of the_hub_ – and all angles will remain the same. Since it’s the angles that we want to compute, we can safely use this simplified model. So we will replace our_base_ with_tmp = base - hub_. You can see the shifted robot in blue on the picture.

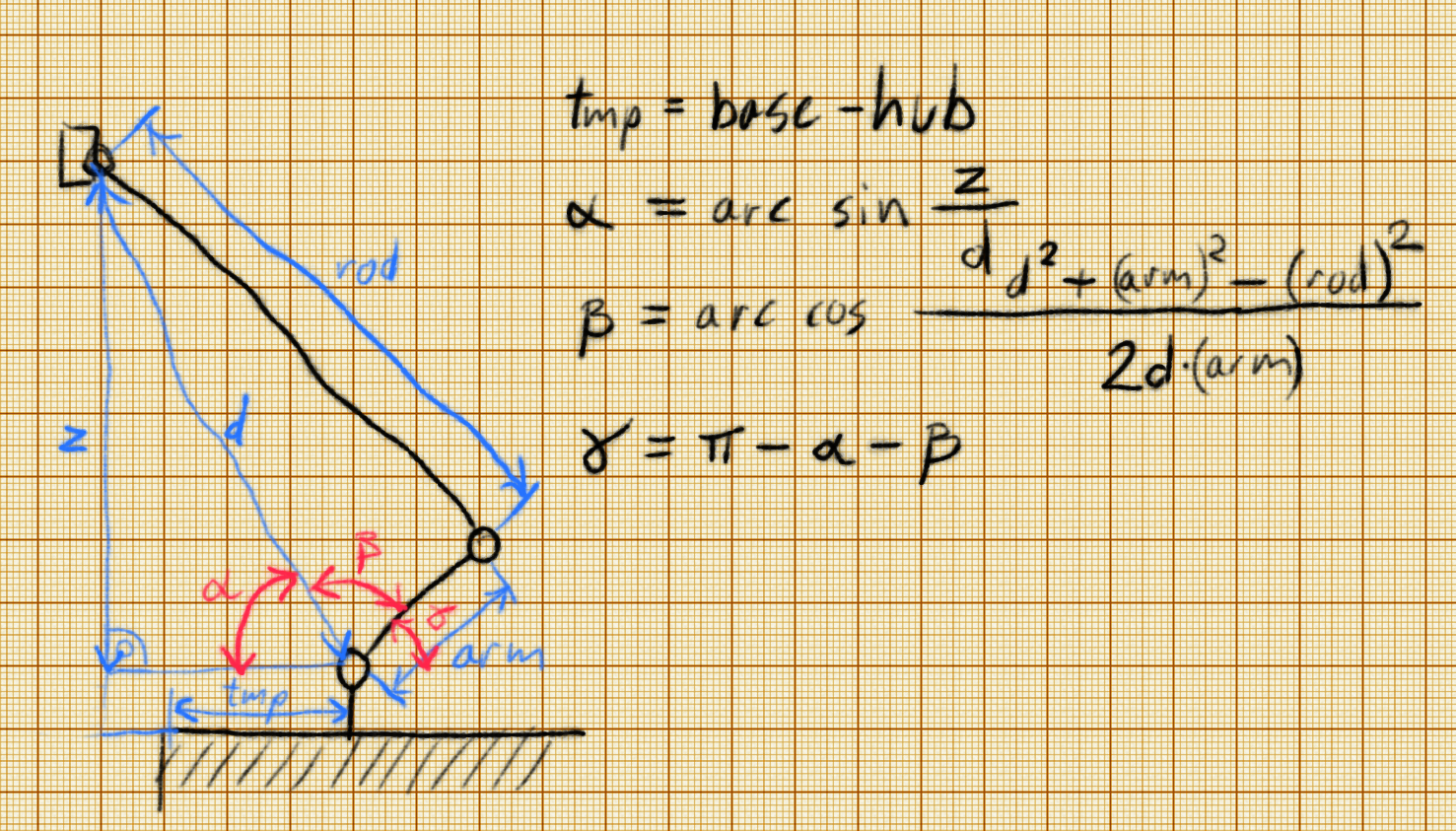
We want to compute the angle γ, but to do that, we will compute angles α and β, and then γ = 180° - α - β. The angle β controls the length of this part of the robot, while the angle α controls its attitude – so that it points towards our tool. All we know is the distance_d_ of the tool to the servo, and the height_z_ of the tool. We also know the dimensions of all the parts of our robot.

We can calculate angle α directly from the definition of the sine function: sin α = z / d. The triangle that β spans is not a right-angle triangle, so we can’t do the same trick. But we know all the sides of that triangle, so we can use the law of cosines to calculate its angles.

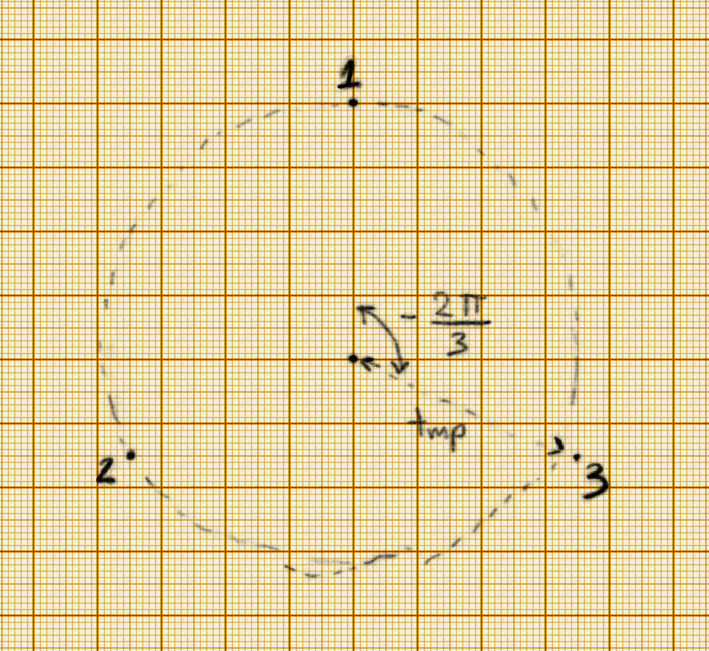
Now, all that is left for us is calculating the z and d for each of the 3 parts of the robot. Actually, z is the same as given in the (x, y, z) coordinates that specify the position of the tool. All we need then is d, which is the euclidean distance between the tool and the servos of each of the parts. The first part is easy: its x coordinate is 0 and its y coordinate is tmp. The other two points are rotated from that by 120° – so their positions are (tmp * sin 120°, tmp * cos 120°) and (-tmp * sin 120°, tmp * cos 120°). The z of all three points is 0.

And that’s it. That’s all that is needed to control this robot.